Minev-Ethier test

The esact solution of Minev-Ethier [ME98] is defined on \(\Omega=[-0.5, 0.5\)^3] by:

\[\begin{eqnarray} u_1 &=& -e^x\sin(y+z) - e^z\cos(x+y)\\ u_2 &=& -e^y\sin(z+x) - e^x\cos(y+z)\\ u_3 &=& -e^z\sin(x+y) - e^y\cos(z+x)\\ p &=& -0.5e^{2x} - 0.5e^{2y} - 0.5e^{2z}\\\nonumber && -\sin(x+y)\cos(z+x)e^{y+z}\\\nonumber && -\sin(y+z)\cos(x+y)e^{z+x}\\\nonumber && -\sin(z+x)\cos(y+z)e^{x+y}\nonumber \end{eqnarray}\]

External forces are calculated using exact solution in the Stokes / Navier-Stokes equations.

Dirichlet conditions

We compare the approximated solution and the exact solution of Bercovier-Engelman, respectively for pressure (Figure 1 and Figure 2) and velocity (Figure 3 and Figure 4).

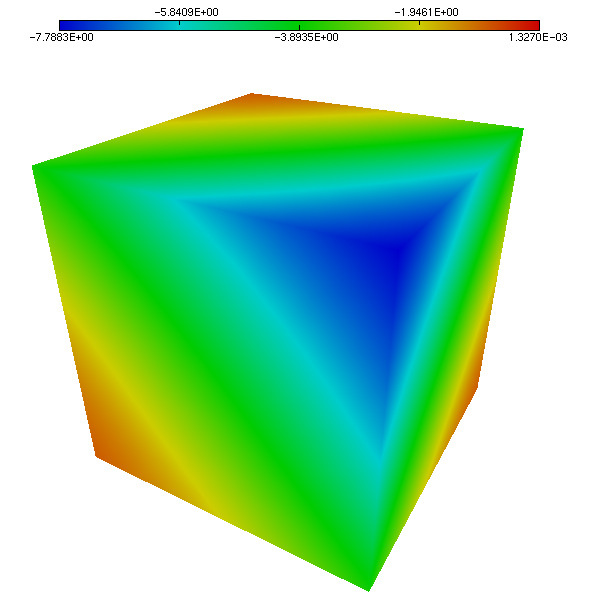
Stokes MR P
Figure 1. Pressure on the unit cube. Computed solution
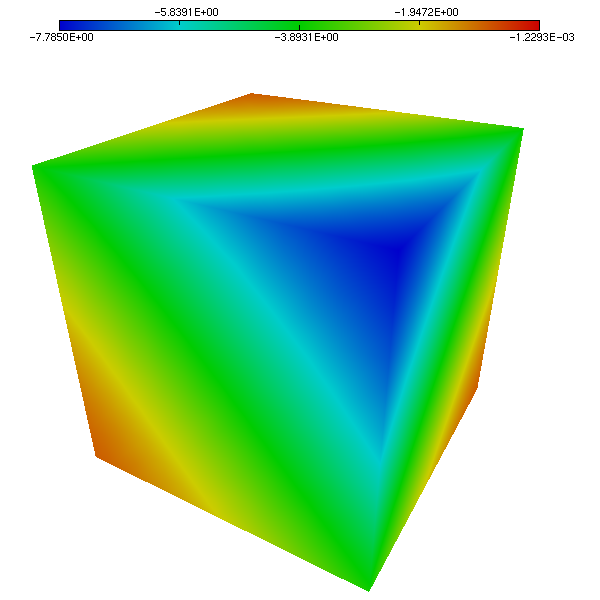
Stokes MR Pexact
Figure 2. Pressure on the unit cube. Exact solution
Stokes MR V
Figure 3. Velocity field on the unit cube on the cut y=0. Computed solution
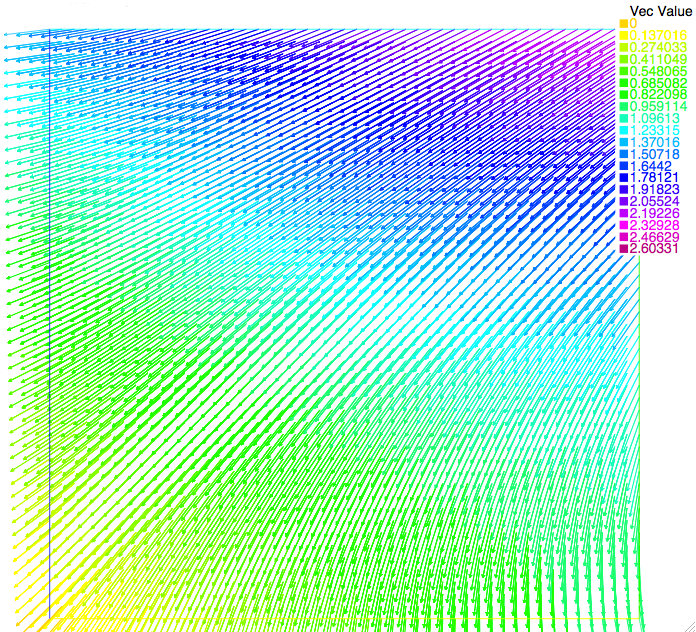
Stokes MR Vexact
Figure 4. Velocity field on the unit cube on the cut y=0. Exact solution

FreeFem++ algorithm:

Mixed conditions

We compare the approximated solution and the exact solution of Bercovier-Engelman, respectively for pressure (Figure 5 and Figure 6) and velocity (Figure 7 and Figure 8).

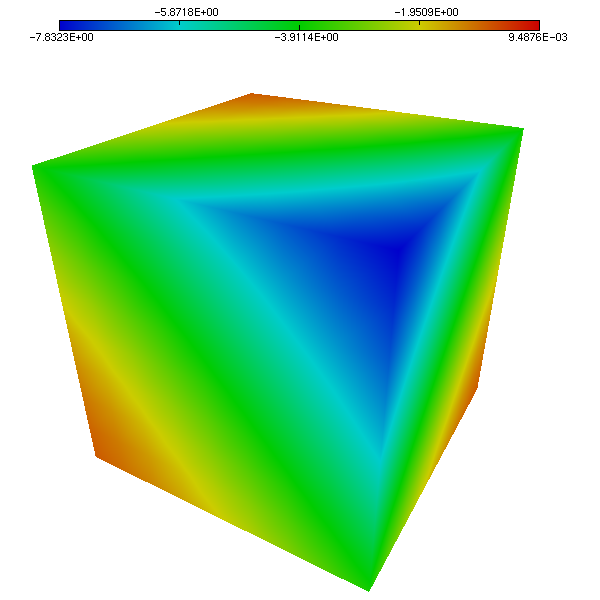
Stokes MR P Mixed
Figure 5. Pressure on the unit cube. Computed solution
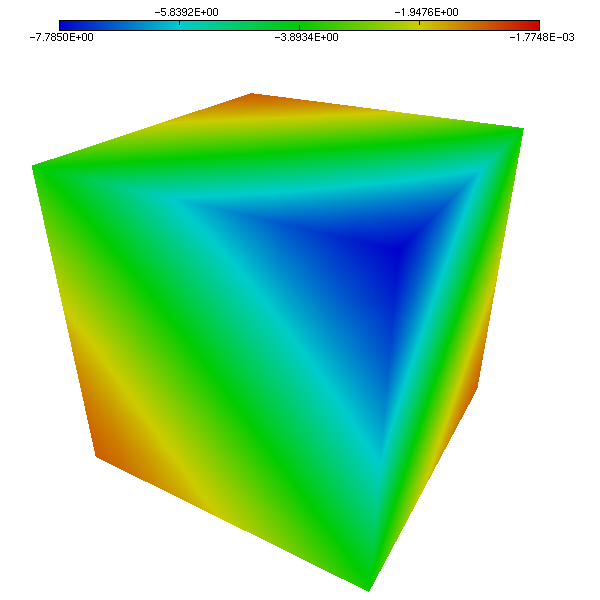
Stokes MR Pexact Mixed
Figure 6. Pressure on the unit cube. Exact solution
Stokes MR V Mixed
Figure 7. Velocity field on the unit cube on the cut y=0. Computed solution
Stokes MR Vexact Mixed
Figure 8. Velocity field on the unit cube on the cut y=0. Computed solution

FreeFem algorithm:

  • Stokes_ME_mixed.edp

  • Navier-Stokes_ME_mixed.edp